Negli ultimi anni l’Istat si è molto impegnata nella divulgazione della Statistica e dell’importanza della cultura statistica organizzando eventi di vario tipo, concorsi per le scuole, festival.
Rivolgendosi ai più piccoli, alcune bravissime ricercatrici hanno realizzato e pubblicato delle Fiabe Statistiche raccolte nei due volumi “Le streghe di Bayes e altre storie” e “Il pavone della pioggia e altre storie”.
Perché questo interessa i genitori?
Al seguente link è possibile leggere e ascoltare alcune fiabe tratte sia dal primo volume che dal secondo.
La fiaba che più mi ha più colpita è Il Dottor BoxPlot; è raccontata davvero bene, come d’altra parte tutte le altre fiabe, e aiuta a comprendere il significato di alcuni tra gli indici statistici che spesso vengono calcolati anche nel caso delle più semplici indagini statistiche, in particolare alcuni indici di tendenza centrale (quartili) e di variabilità (campo di variazione, differenza interquartile).
Il racconto permette di prendere confidenza anche con un tipo di rappresentazione grafica non molto noto, il BoxPlot, con il quale si può riassumere in un’unica rappresentazione grafica proprio tali indici.
La fiaba racconta di un mondo speciale, il pianeta Kepler-1647(AB)b detto anche Tatù, in cui gli abitanti mangiano solo numeri… un mondo dove chissà se mi piacerebbe vivere!!!
Certo che la forma del corpo dei tatùani è un po’ strana: una scatola con solo due braccia, a volte di diversa lunghezza, mani con due dita e un naso che raramente si trova perfettamente centrato.
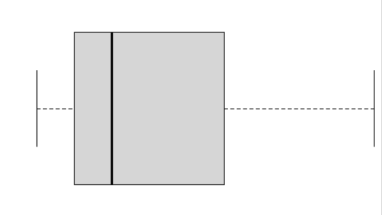
La salute di ogni abitante dipende dalla qualità dei numeri mangiati, o meglio dalla varietà della dieta, cosicché accade che chi mangi sempre gli stessi numeri si ammali di Monotonia Numeraria!!!
Perché la statistica “da favola” interessa gli insegnanti?
Per comprendere meglio e soprattutto per svolgere in modo veloce i calcoli statistici, ci affidiamo a R che troviamo al link, uno strumento potentissimo utilizzato sicuramente da specialisti di statistica, ma decisamente facile per un approccio iniziale: sarà immediato costruire insiemi di numeri, effettuare il calcolo dei suddetti indici e produrre il relativo BoxPlot.
Iniziamo quindi a preparare un pranzetto che, come nella fiaba è accaduto al piccolo Pyloyxt, a lungo andare possa essere causa di Monotonia numeraria: un bel piatto di numeri tutti uguali, come ad esempio 1 1 1 1 1 1 1 1 1 1.
Può essere divertente, e statisticamente utile, immaginare che Pyloyxt disponga su un tavolo gli 1 in fila e che se ne cibi prendendo un 1 alla volta, per gustarselo bene.
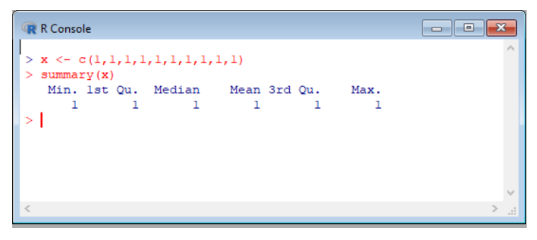
Nella console di R abbiamo costruito una variabile statistica x che nel nostro mondo potrebbe costituire, ad esempio, il risultato di una rilevazione su un campione di unità statistiche che presentino la stessa modalità di un certo carattere, ad esempio “numero di televisori posseduti”: tutti gli intervistati ne possiedono solo 1.
Il comando summary() di R, mostrato nella console, permette di calcolare i principali indici: il Valore Minimo,il Primo Quartile,la Mediana (o Secondo Quartile), il Terzo Quartile, il Valore Massimo. Ovviamente, in questa situazione dove tutti i dati sono uguali anche i valori degli indici sono tutti uguali: non c’è alcuna variabilità!
Che dieta monotona, povero Pyloyxt!!!!
Come sarà il BoxPlot in questa situazione? R ci permette di costruirlo facilmente scrivendo:
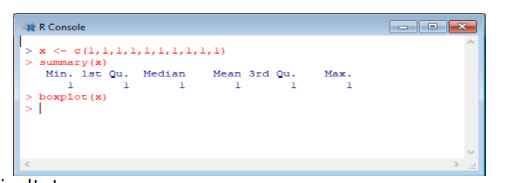
Ed ecco il risultato:
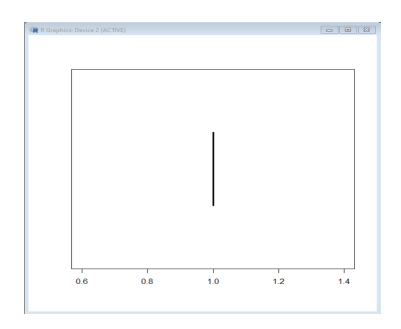
Certo che un abitante di Tatù che mangiasse solo numeri 1 avrebbe un aspetto davvero orribile!!!!
Proviamo allora a variare la sua dieta e a dargli in pasto numeri appena un po’ diversi:
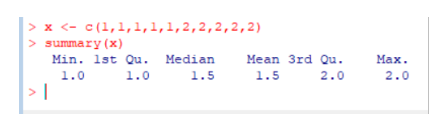
Ed ecco come cambia il suo aspetto:
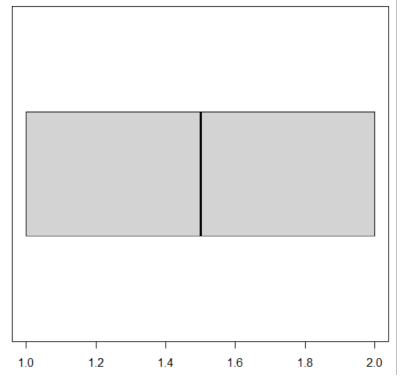
Poverino, ancora senza braccia e mani!!!! ma almeno con un naso ben centrato.
Ma come mai?
Osserviamo il “cibo” e proviamo ad individuare quegli elementi che permettano di dividere la sequenza in 4 parti uguali, proprio come fa R:
1 1 1 1 1 2 2 2 2 2
L’ 1 è il Primo Quartile, cioè il separatore tra il primo gruppo e il secondo; il 2 è il Terzo Quartile e separa il terzo gruppo dal quarto; e al centro?
Per separare il secondo gruppo dal terzo dobbiamo metterci un 1,5, anche se non fa parte del “cibo”, che viene detto Secondo Quartile o Mediana. Sono proprio i valori che vengono calcolati con il comando summary() di R, il quale ci restituisce anche un altro indice, la Media Aritmetica … ma che per qui non ci serve!
In questa particolarissima situazione, il Primo Quartile coincide con il Valore Minimo e il Terzo Quartile con il Valore Massimo.
Ed ecco svelato l’arcano: il corpo del tatùano è una scatola che si sviluppa tra il Primo e il Terzo quartile, mentre le braccia sono tra il Valore Minimo e il Primo Quartile, una, e tra il Terzo Quartile e il Valore Massimo, l’altra. Allargando bene le sue braccia, il nostro amico tatùano ci mostra tutta la sua “apertura bracciale”, o meglio, il suo Campo di Variazione.
Come fare allora per dargli le due braccia? Dovremmo fare in modo che il Primo Quartile non coincida con il Valore Minimo e che il Terzo Quartile non coincida con il Valore Massimo, ad esempio introducendo nella dieta nuovi numeri:
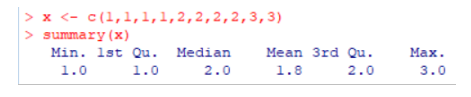
Con un dieta un po’ più varia, un 1 e un 2 sostituiti con due 3, cosa accadrà? Ora il Terzo Quartile è diverso dal Valore Massimo, ma uguale alla Mediana … mumble mumble … vediamo:
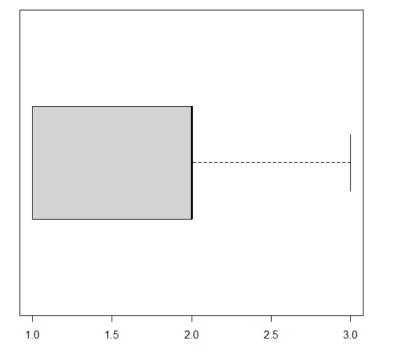
Grandioso! Siamo riusciti a dargli un braccio e una mano!
Ancora un piccolo sforzo, amico tatùano, prova a mangiare un numerino ancora diverso e vedrai che ti sentirai meglio:
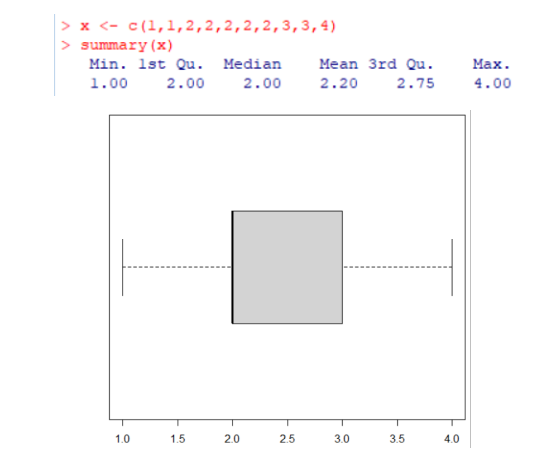
Mica male… dobbiamo aggiustarti ancora un po’ il naso e poi sarai perfetto!
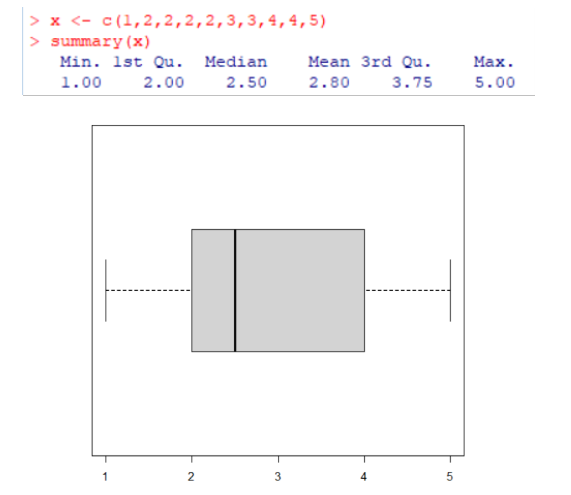
Finalmente, ora sì che sei carino!
Avrete osservato che i tatùani sono piuttosto maniaci dell’ordine e, come abbiamo già detto, ogni volta, prima di mangiare il loro pranzetto quotidiano, i tatùani dispongono in ordine il loro cibo, dal numero più piccolo al numero più grande. Dato che hanno a che fare solo con numeri, la cosa non gli rende poi la vita così complicata.
Certo così non potrebbero mai cibarsi di altro, che ne so, di colori, di nomi, insomma di cose che non si possono metter in ordine.
E chissà se esiste un pianeta dove gli abitanti si cibano invece solo di parole e magari il loro aspetto potrebbe essere:
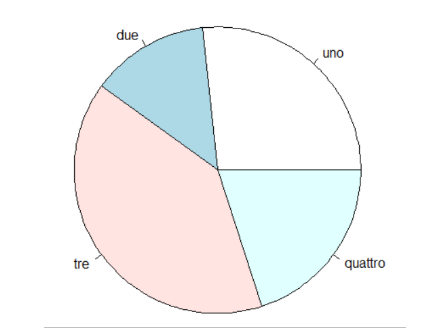
Mi occupo di informatica da circa 40 anni con vari ruoli: studentessa
nella specializzazione Informatica dell'istituto tecnico industriale
quando ancora per programmare si perforavano le schede, poi
programmatrice sui mitici BCS dell'Olivetti, successivamente
Insegnante Tecnico-pratica nella stessa mia scuola. Posso quindi
affermare di essere stata testimone dell'evoluzione dell'informatica
sia dal punto di vista hardware che software.
Mi affascinano molto gli aspetti cognitivi dell'apprendimento e
quindi tutto quanto abbia a che fare con la didattica
dell'Informatica. Ho infatti collaborato con docenti dei vari gradi di
scuola per realizzare progetti informatici, sperimentando approcci
di vario tipo, anche unplugged, e sono stata formatrice per gli
aspetti della didattica digitale nei corsi per docenti neoassunti.
Per passione, ho collaborato come volontaria in un coderdojo.
Mi piace ricordare che la mia prima vera insegnante di informatica
è stata la mia mamma grazie al suo lavoro di sarta e di
ricamatrice.